Zab
This post is about Zab (Zookeeper atomic broadcast) and will cover some relations with Paxos.
Background
Zab is a crash recovery atomic broadcast algorithm designed for Zookeeper. Atomic broadcast is also called total order broadcast - if in a group of processes participating in the broadcast, a process receives m1 before m2 then no other process will receive m2 before m1. Learn more about broadcast algorithms from this video by Martin Klepman.
Zookeeper is a coordination service which is also replicated (it is designed for high throughput and low latency) and requires that a majority of servers have not crashed for progress. In Zookeeper, there is a primary which processes client requests and propagates these state changes in the form of transactions to the backups. During a primary crash there is a recovery protocol before to agree upon a consistent state and a new primary to broadcast state changes (this requires a support of a quorum of nodes). Instance value associated with new primary change. Zookeeper state changes are incremental and are dependent upon previous state so they cannot be applied in a random order (for example think of the state being a db, changes cannot be applied in any order). Also a state change in idempotent i.e applying a state change multiple times will not result in inconsistencies. Zookeeper had some requirements that needed to be considered while designing the broadcast algorithm.
- Multiple outstanding transactions: Zookeeper allows multiple operations to be outstanding (clients submits them) and these should be committed in FIFO order. Paxos tranditionally does not have this feature directly. In the Paxos made simple paper, Implementing a State machine section, when creating a replicated state machine and sending multiple transactions there is a possibility of having gaps which are filled by No-Op commands. (Note there may be other variants of Paxos that are designed handle this, but we are using this vanilla version to compare). Also this Zab paper describes a scenario of accepting different requests by various acceptors, where they are not in the required order as per some dependency. This could be solved by putting dependent transactions in the same paxos proposal, but they affect throughput and latency. Thus this cannot be used due to the nature of the operations in Zookeeper as they are incremental and dependent upon previous operations.
- Efficient recovery: There should be an efficient and fast recovery process, for that each transaction is identified by a pair: instance value and position of the given transaction. So a new primary can just ask the process having the highest transaction identifier and copy the required transaction. However in Paxos the proposer/primary has to execute a phase 1 (sending a prepare request) for all the transactions that it has not learned a value.
Definitions
Let P = {p1, p2, …. pn} be the set of processes in our system with each one having a stable storage and they can do down and may or may not recover randomly.
- A quorum system Q over P is defined such that 1) for all S in Q, S belongs to P and 2) for all Q1, Q2 in Q, Q1 union Q2 is not empty i.e there are common elements.
- Processes use channels to communicate cij between pi and pj, a call from pi to send a message m to pj is send(m, pj) places m in the output buffer of pi for cij. recv(m, pi) gets the next message from pi in the input buffer. Let σi,j,k,k’ be a sequence of messages that pi sent to pj during iteration k of pi and k’ of pj.
- The channels have the following properties 1) Integrity: pi receives m from pj iff pj has sent m 2) Prefix: If pi send ms and there is a m’ s.t. m’ < m (squeezed less than, total order) in σi,j,k,k’ the pj gets m’ before m. Single iteration: the input buffer of pj for channel cij contains messages from at most 1 iteration.
Zookeeper uses a primary backup scheme to execute requests and propagates state changes to backups using PO atomic broadcast (primary order) provided by Zab in which only the primary is able to broadcast. There is a requirement that a mechanism exists to select a primary and guarantee that only one primary exists. Different processes can become primaries and even the same process can become multiple times but they all differ as each refer to a different instance.
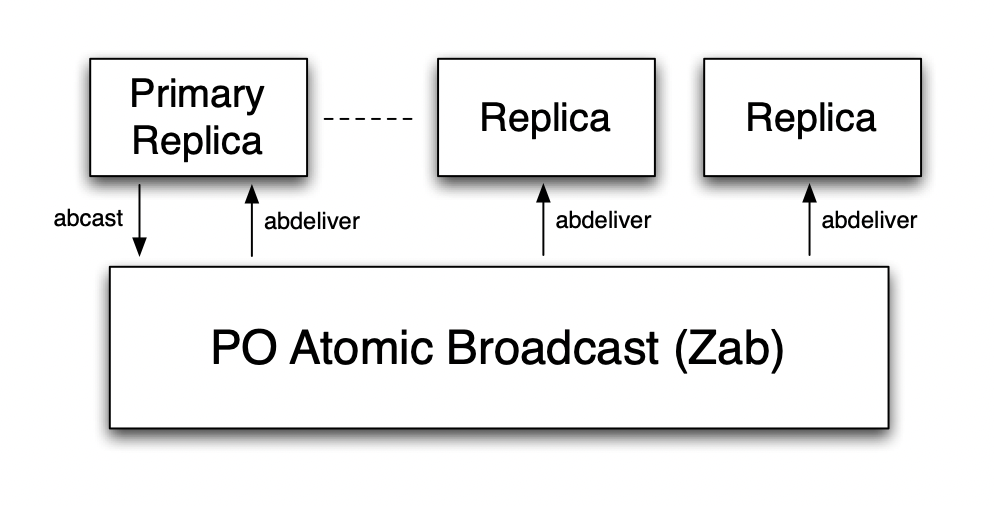
To have the transactions broadcasted by the primary to be consistent the primary should only start once the recovery mechanism (note this is different from the primary picking mechanism) is complete. So when the recovery is complete the Zab layers calls the ready(e) to signal the application(primary and backups) that they can start broadcasting state changes. Using this ready call the application sets its instance value (which is guaranteed to be unique by Zab). A transaction is a state change that the primary wants to propogate is <v, z> v is the transaction value and z is transaction identifier. z = <e, c> e is the epoch number and c is a counter. For a primary pe epoch(z) = instance value = e and on each new transaction the counter c is incremented. Broadcast is done by calling abcast(<v,z>) and delivery to the application is done when it calls abdeliver(<v, z>) [TODO clarify how does a replica get z]. The abcast is not guaranteed to succeed if the primary crashes or changes.
Primary order
Zookeeper requires the following properties:
- Integrity: if some process delivers <v, z> then some process p in P has broadcast <v, z>
- Total order: If some process delivers <v, z> before <v’, z’> ,then any process that delivers <v’, z’> must also deliver <v, z> and deliver <v, z> before <v’, z’> These two guarantee that no transaction spontaneously and processes deliver transaction in an consistent order. Although two processes can have disjoint runs (each delivering separate sequences of transactions). So we have an agreement property.
- Agreement: If a process pi delivers <v, z> and a process pj delivers <v’, z’> then either pi delivers <v’,z’> or pj delivers <v, z>
These three safety properties guarantee that processes are consistent. We have to satisfy the dependency property based on the operations received by the primary i.e if a state change is skipped its dependent states must also be skipped. This property is the primary order property.
- Local Primary Order: If a primary broadcasts <v, z> before <v’, z’> then a processes which delivers <v’,z’> must deliver <v, z> before <v’,z’>
- Global Primary order: If a primary pi broadcasts <v, z> and a primary pj (pi < pj, pj became a primary at some later time than pi) broadcasts <v’, z’> then if a process delivers both <v, z> and <v’, z’> then it must deliver <v, z> before <v’,z’>.
The local primary order preserves FIFO for a single primary and the global primary order help prevent a situation in Paxos where acceptors may loose requests when new proposer comes. (situation explained in a figure is clear to understand). Now the primary should have delivered previous epoch’s (i.e. by the previous primary) transactions before it can begin to broadcast.
- Primary integrity: If a primary pe broadcasts <v, z> then the primary and some process delivers <v’, z’> such that <v’, z’> was broadcast by pe’ (e’ < e) then pe must deliver <v’, z’> before it broadcasts <v, z>.
Comparison with Causal Broadcast
PO atomic broadcast preserves the causal order that occurs in the generation of incremental transactions. Although this is not the same as the causal atomic broadcast.
Causal Atomic Broadcast is defined as: If the atomic broadcast of <v, z> happens before <v, z’> then if a process delivers <v’, z’>, then it should deliver <v, z> before <v’, z’>.
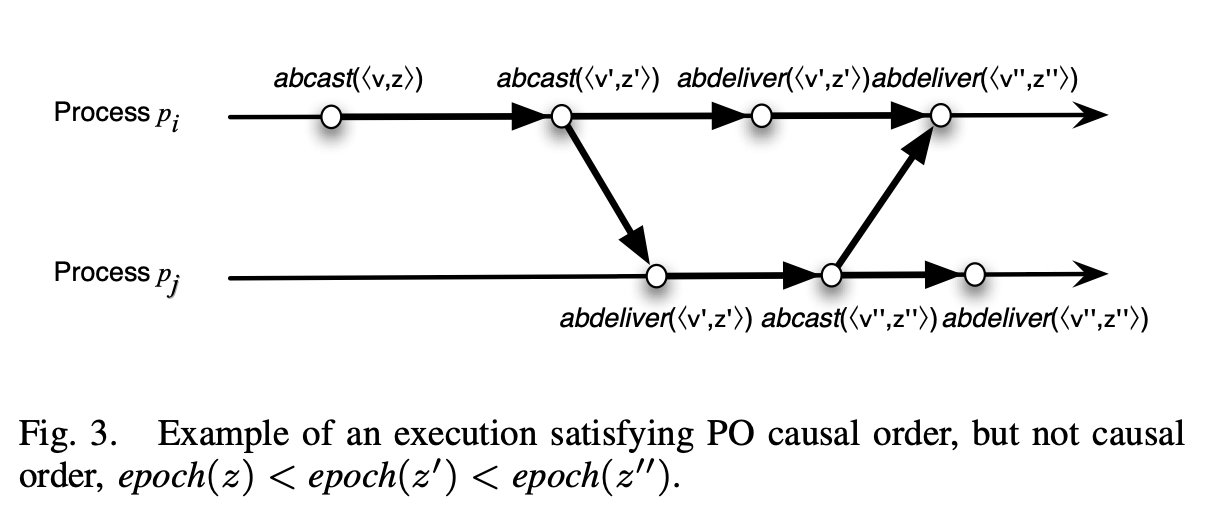
Now, if you observe PO atomic broadcast this is not enforced in Global Primary order Eg in the figure above if pi broadcasts <v, z> and then if it fails and it gets elected again and broadcasts <v’, z’> in another epoch, then if no processes delivers <v, z> then it is acceptable and <v’, z’> can be delivered independently. So this type of dependency between causal broadcast order and mandatory delivery across epochs is not present.
So this order, called as Primary causal order is strictly weaker than causal order. Transactions sent by different primaries are not considered causally related. PO precedence relation is defined as:
An event e PO-precedes another event e’ (e ->po e’) if one of the following conditions hold:
- e and e’ are local to the same process and e occurs before e’ and (e != abcast(<v, z>) or e’ != abcast(<v’, z’>) or epoch(z) != epoch (z’))
- e = abcast(<v, z>) and e’ = abdeliver(<v, z>)
- There is an event e’’ such that e ->po e’’ and e’’ ->po e’
PO causal order is defined as using this ->po instead of “happens before” in the causal order definition. PO atomic broadcast also implements strict causality:
If a process delivers <v, z> and <v’, z’> then either <v’, z’> ->po <v, z> or <v, z> ->po <v’, z’>.
This is needed as transaction are state updates that have to incrementally updated and have to be related, with causal order, there can be transactions delivered that are not causally related. (There is a diagram that gives an example of this)
Algorithm
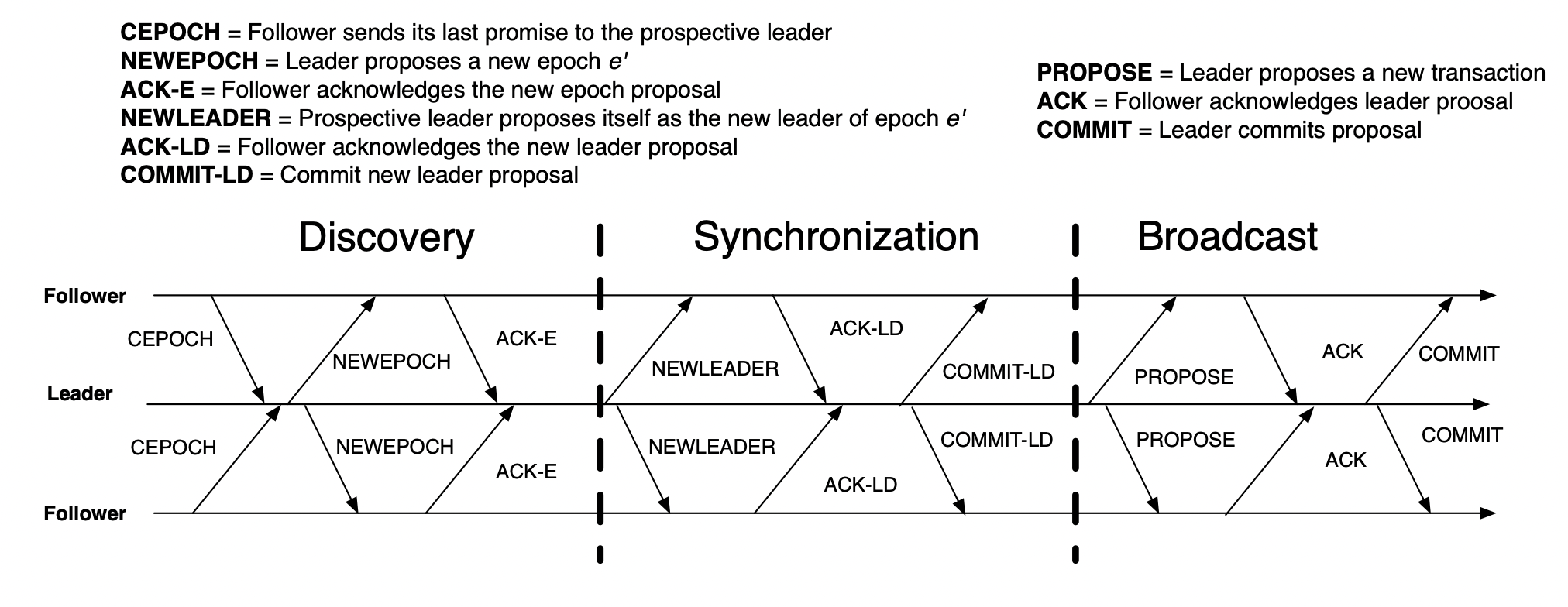
Zab protocol has 3 phases: discover, synchronize and broadcast and each process can perform two roles leader and follower. The leader follows the primary role and proposes transactions called out in the order of the primary. Followers accepts transactions according to the steps of the protocol, this is also done by the leader. Each process implements a leader oracle (Not sure what this is, mostly a separate leader election that outputs some process as leader) to get prospective leader it should follow. If the leader returned by the oracle is itself then to establish leadership it should complete the synchronization phase.
Phase 1: Discovery
- A follower f sends to the prospective leader l its last promise (last accepted epoch no).
- Upon receiving messages from a quorum Q of followers, the prospective leader proposes a new epoch no e’, greater than any received from its followers.
- Followers upon receiving the new no accept/store if its greater than the last promise stored and send back an acknowledgment with current epoch number that it has and the history of transactions.
- Once the leader receives confirmation from each follower in Q, it selects a history of one follower to be the initial history of the next epoch e’ (this follower has the most updated history).
Phase 2: Synchronization
- The prospective leader l proposes a message with new epoch no e’ and the initial history of transactions for this epoch
- when a follower receives this message, it sets the current epoch to be e’ and accepts the transactions that are present in the history and sends an acknowledgement to the follower.
- On receiving ack from quorum of followers, it sends a commit message to all its followers
- On receiving the commit message, the followers deliver the transactions in initial history by invoking abdeliver (Zab layers calls this on the replica - check th figure shown earlier)
Phase 3: Broadcast
- The leader proposes to all followers in Q in increase order of transaction ids (z) a proposal <e’, <v, z» epoch(z) = e’ and it succeeds previously broadcasts in e’
- On receiving ack from a quorum of followers to the proposal the leader sends a commit message for that follower
- A followers call ready(e) if they are leading - this is called by zab layer to let the application layer know that Zab layer is ready to broadcast.
- A follower accepts a proposal and appends to it history
- A follower commits a transaction when it receives a commit message by invoking abdeliver
- If any new follower joins, it will start by sending the prospective leader a message with it last promise as in phase 1 step 0, upon which the new leader starts by sends a message with the new epoch and initial transaction history + the broadcast values
- Upon receiving an ack for the above message from a follower, the leader would send a commit message and adds this follower to the quorum.
Algorithm Implementation Details
- All processes start in a ELECTION state after which one of them moves to LEADING and the rest FOLLOWING state.
- The delivery protocols is similar to 2 Phase commit without aborts - the primary replica picks transactions in FIFO order, the leader on receiving a requests to broadcast the transaction proposes it in increasing transaction id order, the followers accept and ack (after writing to stable storage), once a quorum of proposers have accepted, the leader sends commit on which the followers send any undelivered proposals first then the current one.
- The leader and the primary have different meaning, but co-locating them on the same process has advantages, like a single election to determine both.
- A leader election is run to output a new process as a leader. (This is separate system?, I am not sure of the interaction here or the leader election algorithm used) Processes when they know their “prospective leader” by looking at the output of the leader election algorithm they start Phase 1 in the next iteration.
- The elected leader collects the latest epochs from a quorum of followers and then proposes a later epoch and collects the highest transaction ids. The leader completes its phase-1 once it gets the follower with the most updated history of transactions (highest id).
- Steps in phase-1 guarantee that none of the followers in Q accept proposals from earlier epochs. Also the leader only copies any missing transaction from leading follower.
- In phase-2, the elected leader proposes itself as a leader and also after this process the followers lagging behind would be having the same initial state of transactions.
- Leaders propose operations by queueing them to each of the followers. The leader and followers exchange heartbeats. If the leader does not receive a heartbeat from a quorum of followers within an interval, it moved back to the ELECTION state and starts a new iteration of the algorithm.
- Similarly if the follower does not receive the heartbeat within the timeout interval is abandons the leader and moves to the ELECTION state. Also if any new leader has been established and the initial history wrt the new leader has been committed any the other NewLeader messages are ignored.
Will not go into the proofs as of now, if I do visit it later, i’ll update it here.
Note
- Please let me know if I misinterpreted or missed something.
`