Paxos
My understanding of the Paxos consensus protocol through the paper Paxos Made Simple. The Paxos lecture video by the creators of Raft is really helpful.
Introduction
A consensus algorithm to ensure that a single value is chosen by the processes/nodes from the proposed values. The three agents in this consensus algorithm are proposers, acceptors and learners. Communication happens by sending messages in the asynchronous, non-Byzantine (no malicious nodes) model with the agents failing, stopping or restarting arbitrarily and no bounds on message delivery, losses. This vanilla Paxos is used for reaching consensus on a single value.
Properties
Safety:
- Only a value that has been proposed may be chosen
- Only a single value is chosen
- A process never learns that a value is chosen unless it has been
Liveliness (paper does not focused on this as such):
- Some proposed value is eventually chosen
- If a value has been chosen, then a process can eventually learn the value
Choosing a value
We cannot have a single acceptor to choose a value, as if it fails the system halts indefinitely. So consider multiple acceptor agents, a proposer send a value to a set of acceptors and an acceptor may accept the proposed value. The value is considered to be “chosen” when its “accepted” by a majority of the acceptors (quorum). If we have this base requirement to choose a value when only a single value is proposed by one proposer -> P1: An acceptor must accept the first proposal it receives, we face issues when multiple values are proposed (value accepted by different acceptors and no majority). So we should allow the acceptors to accept more than one proposal.
But there has to be some order/protocol in which the acceptors accept proposals, as if they accept all proposals they get, then multiple values can be chosen. So to keep track of the proposals, assume we have proposal numbers (different proposers have different numbers) attached to proposals. Allowing multiple proposals and to guarantee the same chosen value later gets us this requirement: P2: If a proposal with value v is chosen, then every higher-numbered proposal that is chosen has the value v. Considering that acceptance is needed before choosing, P1 and to avoid proposers producing higher numbered proposals with different value than the one chosen, we require P2b: If a proposal with a value v is chosen, then every higher-number proposal issued by any proposer has value v.
To ensure this, let’s think how we would try to prove this. Assume the hypothesis P2b is true for all proposal no. up to n-1 with the base condition that a proposal with no m with value v that is chosen. Then if another proposal comes along with no n > m it should also have the value v. By induction on n, we have the proposals with no’s from m…(n-1) have value v. Let C be the majority set of acceptors that have chosen v. Thus, every acceptor in C has accepted a proposal with number in m…n-1 and every proposal with no in m…n-1 accepted by any acceptor has value v. We can conclude that a proposal numbered n will have value v by ensuring that the following invariant/requirement is maintained P2c: “For any v and n, if a proposal with value v and no n is issued, then there is a set S consisting of a majority of acceptors such that either (a) no acceptor in S has accepted any proposal numbered less than n or (b) v is the value of the highest-numbered proposal among all proposals numbered less than n accepted by acceptors in S”. Once we have P2c maintained we know any S in this proof, a majority set of acceptors would have at least one acceptor in C. So it is only possible that b) condition holds and the proposal numbered n will have value v (that is the value of the proposal accepted by C numbered less than n i.e. in between m…n-1).
To maintain the invariance of P2c, the proposer issue the proposal numbered n should learn about the highest numbered proposal less than n. Another intuition for this is like a 2 phase protocol, the proposers should know if other values are accepted/chosen from other proposals before sending their own. A proposer can learn about an already accepted value from the acceptor, but it has to be sure that a future proposal is not accepted in the time it sends its proposal. So the proposer extracts a promise by requesting the acceptor not to accept proposals numbered less than n, this is a prepare request with n. In the response the acceptors agrees to not accepts a proposal numbered greater than n and send the proposal value and number if its has accepted any. If the proposer receives a response from the majority it can then issue a proposal with n and v (the value from the highest-numbered proposal among the responses, to maintain P2c). An acceptor can accept a proposal numbered n iff it has not responded to a prepare request having a number greater than n. Once a majority have responded to the accept request (by returning that they have accepted n), the value is chosen.
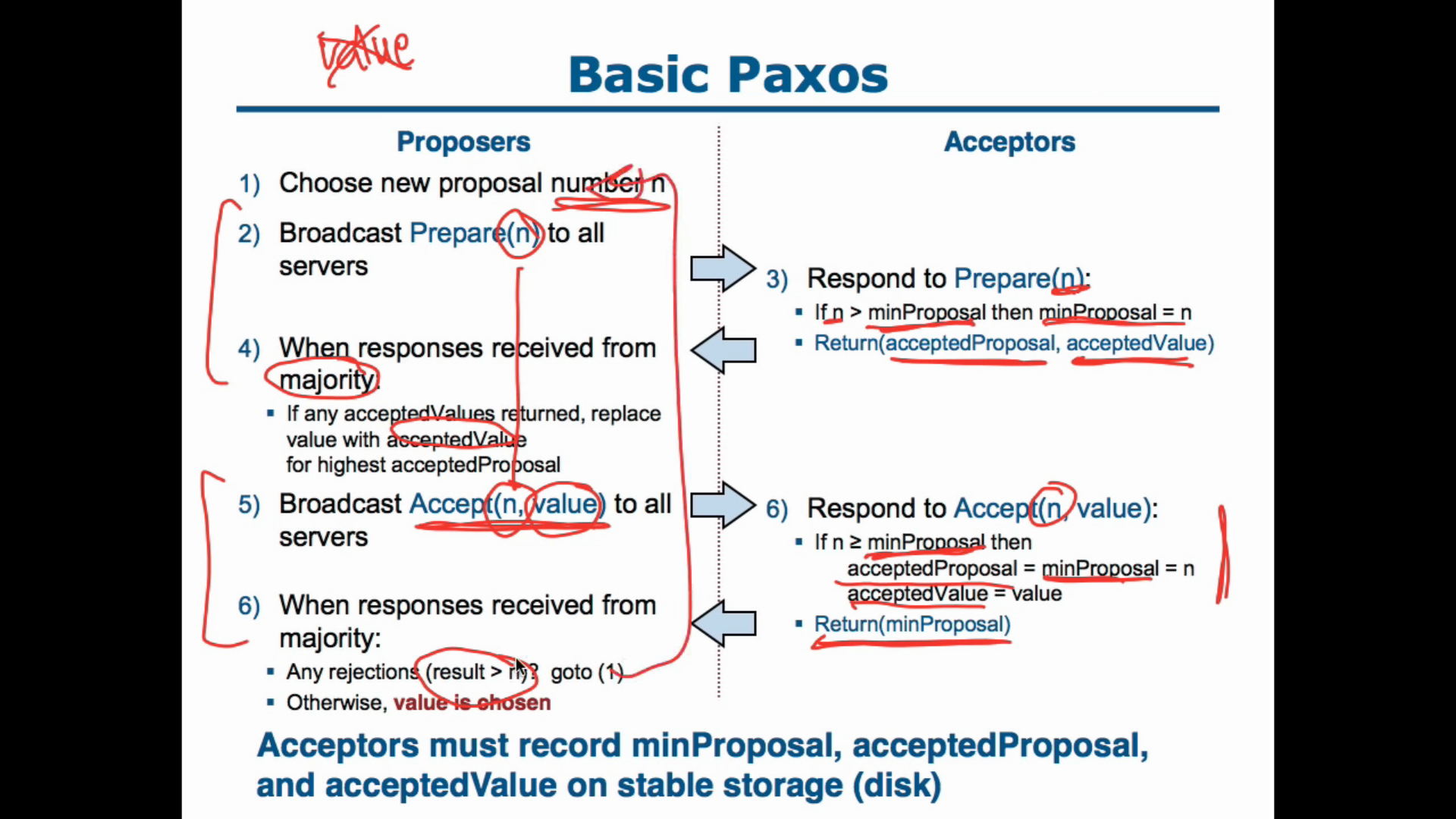
The algorithm to choose a value is described above. There are other optimizations that are/can be done like the acceptor can ignore prepare requests with number less than already promised, these will not affect the correctness of the algorithm. To maintain P2C regardless of failures, the acceptor must save highest-numbered proposal that it has ever accepted and the number of the highest-numbered prepare request to which it has responded.
Learning and Progress
Until now this algorithm is safe, has all the safety properties. However, to have the liveliness properties there are some other things to consider. First for learning the chosen values, the acceptors can send the accepted values to all the learners (just another terminology in the paper, nodes can be all learners, acceptors and proposers). This will have the learners know about the chosen value the fastest but with a lot of communication overhead. Another option is to have a set of designated/distinguished learners that acceptors will send to, and they will forward the value to the other learners. Learners can also issue a proposal to know about a chosen value if they need to.
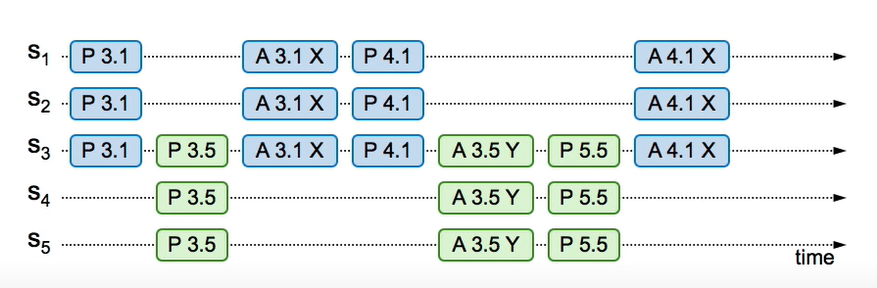
Now, paxos as described above would not have a guarantee to converge/terminate, a value to be chosen. Consider the diagram below, where the proposers cancel each other’s proposal with the prepare request having higher-number of one proposer coming before proposal/accept of the other. To solve this there has to be done randomness introduced before proposers send requests or as stated in the paper we have to elect a leader - a distinguished proposer that proposes a value. And in this asynchronous and non-Byzantine model it must use some timeouts. etc to prevent failures and have a leader election (a specific way to do that is not mentioned in the paper). Thus, given FLP impossibility, we cannot have an distributed consensus algorithm that is always safe and live. Paxos is always safe and is live during periods of synchrony (when leader is elected successful)
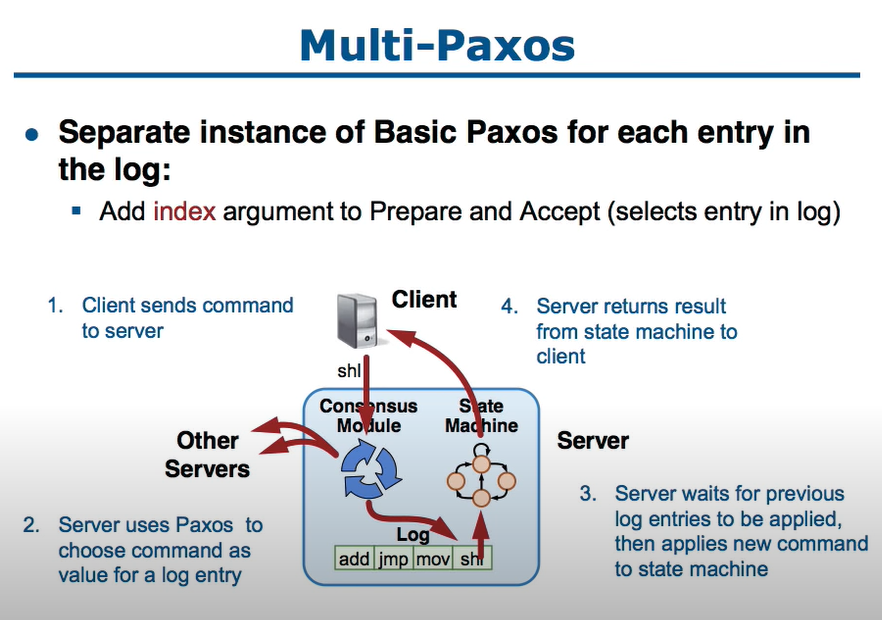
Further the paper describes using multiple rounds of Paxos for selected multiple values (Multi-Paxos) and implementing a state machine on multiple servers. As in the image shown below the aim is to have a single leader proposer and to have clients send their commands to the proposer. The proposer gets the command as a value chosen for a particular entry in a log. Once the log has the entry i.e. chosen by Paxos, the commands can be given to the state machine in a serial order. The proposer can propose multiple commands received (after all commands before that are chosen) to be stored at different log index and failures to get it chosen in between may lead to gaps. These and leader failures must be handled.
I won’t dive into this for now, instead I will go over to the Paxos made live paper to explore practical usage in the next post.
Versus
A more comprehensive section is possible here.
Paxos is more fault tolerant than other consensus algorithms like 2PC (brief in the Designing Data Intensive Applications Summary). It does not block as long as majority of processes are alive (withstand f failure withi 2f + 1 acceptors) unlike 2PC with blocking coordinator failure.
Note
- Please let me know if I misinterpreted or missed something.